c言語を再履修した俺でもわかる制御工学シリーズ-3
c言語でわかる制御工学-その3:一次遅れのPI制御
こんにちは、今回はついにRC回路のPI制御です。一次遅れの伝達関数を持つシステムをPI制御しようと思います。
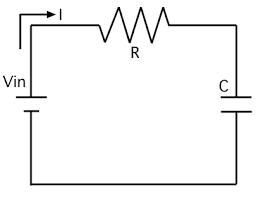
それでは、PI制御について簡単に説明します。まずはプログラムを読んでみてください。
さて、まずはじめにPI制御の概要について説明します。入力は比例動作と積分動作の和になります。
[制御入力] = [比例動作] + [積分動作]
比例動作のゲインをPとすると、比例動作は偏差を比例ゲインで掛けたものになります。
[比例動作] = P*[偏差]
次に積分動作についてです。積分動作のゲインをIとすると、積分動作は入力を開始した時刻0から現在の時刻までの偏差の時間積分に、積分ゲインを掛けたものになります。
実際にゲインのパラーメーターを変更することで、応答にどのような変化が起こるのかを実験します。P=1.0, I=1.0, 目標値は前回同様1.0です。
この時、出力結果は、オーバーシュートなし、±5[%]の制定時間は3.00[s]でした。
TIME=3.00 Vo=0.950207
実は、この時の応答は、R=C=1.0のステップ応答にほぼ一致します。
(下の結果は第一回目のステップ応答のプログラムを0.01刻みに変更しています)
[ステップ応答]
TIME=1.000000 Vo=0.633968
[PI制御]
TIME=1.00 Vo=0.635809
これは零点と極が一致したために起こったことですが、これについて詳しくは次回にします。
次にP=1.0で固定して、Iの値を変化させることで、応答がどう変化するのかを実験してみましょう。
Iを大きくするとオーバーシュートが発生するので、Tdを行き過ぎ時間、P.Oをパセントオーバーシュートとして、応答を評価します。
GAIN_P=1.000000 GAIN_I=2.000000
Td=2.34 P.O=6.6109[%]
GAIN_P=1.000000 GAIN_I=3.000000
Td=1.77 P.O=13.6034[%]
GAIN_P=1.000000 GAIN_I=4.000000
Td=1.50 P.O=19.0387[%]
このように、I=1.0から少しずつIを大きくすると、Tdが小さくなり、P.Oは大きくなります。つまり、速応性は上がるものの、オーバーシュートは増加し不安定になります。
では逆にI=1.0から少しずつIを小さくすると、どをのように変化するのでしょうか試してみましょう。
GAIN_P=1.000000 GAIN_I=0.500000
オーバーシュートなし。±[5]制定時間8.00[s]
GAIN_P=1.000000 GAIN_I=0.100000
オーバーシュートなし。±[5]制定時間44.90[s]
このように、Iを小さくするとオーバーシュートはなくなり、応答は遅くなっていきます。
では、次にI=1.0に固定してPを大きくします。すると、オーバーシュートなくなり、応答が速くなります。これは一次遅れのステップ応答に似ているので、出力が63.2[%]になるまでにかかる時間で応答の特性を評価します。
GAIN_P=2.000000 GAIN_I=1.000000
TIME=0.60 Vo=0.634370
GAIN_P=3.000000 GAIN_I=1.000000
TIME=0.39 Vo=0.631785
GAIN_P=4.000000 GAIN_I=1.000000
TIME=0.28 Vo=0.628745
このように、Pを大きくするほど出力が63.2[%]が小さくなるので、応答が速くなることがわかりました。
今度はPを1より小さくするとオーバーシュートが発生します。
GAIN_P=0.500000 GAIN_I=1.000000
Td=4.01 P.O=3.4041[%]
GAIN_P=0.100000 GAIN_I=1.000000
Td=3.64 P.O=12.6041[%]
このように、Pを小さくするほどオーバーシュートは大きくなるが、行き過ぎ時間Tdは小さくなるため、速応性は上昇したとわかります。
この結果から、Pを1より大きくしても小さくしても速応性は上昇するという結果がわかりました。
内容が膨大になるため、今回の実験でなぜこのような結果になったのかは説明しませんでした。次回は今回の結果を、制御系全体の閉ループ伝達関数の極と零点から説明したいと思います。